|
ФИиУ
Надёжность
КБГУ
КБГУ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3.5.4. Пример определения показателей надежности неремонтируемого объекта по опытным данным 3. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ, НАИБОЛЕЕ ЧАСТО ИСПОЛЬЗУЕМЫЕ В РАСЧЕТАХ НАДЕЖНОСТИ Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рис. 3.1), соответствующих трем периодам жизни этих устройств [3, 8, 10, 19].
Нетрудно увидеть, что этот рисунок аналогичен рис. 2.3, так как график функции l (t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла [12, 13, 15]. Согласно этому распределению плотность вероятности момента отказа
где d - параметр формы (определяется подбором в результате обработки экспериментальных данных, d > 0); l - параметр масштаба, 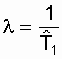 . .Интенсивность отказов определяется по выражению
Вероятность безотказной работы
а средняя наработки до отказа
Отметим, что при параметре d= 1 распределение Вейбулла переходит в экспоненциальное, а при d= 2 - в распределение Рэлея. При d<1
интенсивность отказов монотонно убывает (период приработки), а при Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме [12]. 3.2. Экспоненциальное распределение Как было отмечено в подразд. 3.1 экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы d = 1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра l = const . Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:
Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:
Заменив в выражении (3.5)
величину
l величиной
1 / Т1, получим
Таким образом, зная среднее время безотказной
работы Т1 (или постоянную интенсивность отказов l
), можно в случае экспоненциального распределения найти вероятность безотказной
работы для интервала времени от момента включения объекта до любого заданного
момента t.
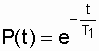 .
(3.7) .
(3.7)Отметим, что вероятность безотказной работы на интервале, превышающем среднее время Т1, при экспоненциальном распределении будет менее 0,368: Р(Т1) =
Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т1, то есть интервал времени на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы. Как известно [4, 13], если для случайной величины t задана плотность вероятности f(t) и определено среднее значение (математическое ожидание) Т1, то дисперсия времени безотказной работы находится по выражению:
и для экспоненциального распределения соответственно равна:
После некоторых преобразований получим:
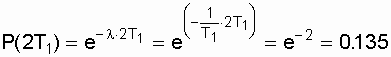 . .Важно отметить, что если объект отработал предположим, время t без отказа, сохранив l = соnst, то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения l = соnst. Таким образом, отключение работоспособного
объекта в конце интервала Другие распределения не имеют указанного свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод: поскольку за все время t устройство не стареет (не меняет своих свойств), то нецелесообразно проводить профилактику или замену устройств для предупреждения внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой парадоксальности этот вывод не содержит, так как предположение об экспоненциальном распределении интервала безотказной работы означает, что устройство не стареет. С другой стороны, очевидно, что чем больше время, на которое включается устройство, тем больше всевозможных случайных причин, которые могут вызвать отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится выбирать интервалы, через которые следует производить профилактические работы с тем, чтобы сохранить высокую надежность работы устройства. Этот вопрос подробно рассматривается в работе [1].
Модель экспоненциального распределения
часто используется для априорного анализа, так как позволяет не очень сложными
расчетами получить простые соотношения для различных вариантов создаваемой
системы. На стадии апостериорного анализа (опытных данных) должна проводиться
проверка соответствия экспоненциальной модели результатам испытаний. В
частности, если при обработке результатов испытаний окажется, что На практике часто бывает, что l№const,однако, и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить [12, 15] средним значением: l (t) "lcр(t) = const. Плотность вероятности в законе Рэлея (см. рис. 3.4) имеет следующий вид ¦ где d* - параметр распределения Рэлея (равен моде этого распределения [13]). Его не нужно смешивать со среднеквадратическим отклонением:
Интенсивность отказов равна:
Характерным признаком распределения Рэлея является прямая линия графика l(t), начинающаяся с начала координат. Вероятность безотказной работы объекта в этом случае определится по выражению
Средняя наработка до отказа
3.4. Нормальное распределение (распределение Гаусса) Нормальный закон распределения характеризуется плотностью вероятности вида
где mx, sx - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х. При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать mx и sx. Вероятность безотказной работы определяется по формуле
а интенсивность отказов - по формуле
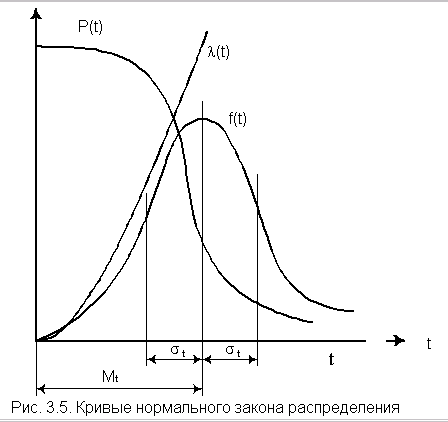
На рис. 3.5 изображены кривые l(t), Р(t) и¦ (t) для случая st<< mt, характерного для элементов, используемых в системах автоматического управления [3].
В данном пособии показаны только наиболее
распространенные законы распределения случайной величины. Известен целый
ряд законов, так же используемых в расчетах надежности [4, 9, 11, 13, 15,
21]: гамма-распределение, Следует отметить, что если неравенство st<< mt не соблюдается, то следует использовать усеченное нормальное распределение [19]. Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом. В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в [13,15], при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений (см. разд. 8). 3.5. Примеры использования законов распределения в расчетах надежности Определим показатели надежности для наиболее часто используемых законов распределения времени возникновения отказов. 3.5.1. Определение показателей надежности при экспоненциальном законе распределения Пример. Пусть объект имеет экспоненциальное распределение времени возникновения отказов с интенсивностью отказов l = 2,5 Ч 10-5 1/ч. Требуется вычислить основные показатели надежности невосстанавливаемого объекта за t = 2000 ч. Решение.
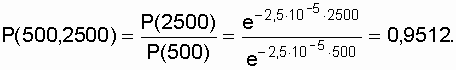 . .
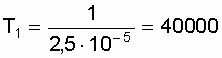 ч. ч.3.5.2. Определение показателей надежности при распределении Рэлея Пример. Параметр распределения d* = 100 ч. Требуется определить для t = 50 ч величины P(t), Q(t), l (t),Т1. Решение. Воспользовавшись формулами (3.11), (3.12), (3.13), получим
3.5.3. Определение показателей схемы при распределении Гаусса Пример. Электрическая схема собрана
из трех последовательно включенных типовых резисторов:
Требуется определить суммарное сопротивление схемы с учетом отклонений параметров резисторов. Решение. Известно, что при массовом производстве
однотипных элементов плотность распределения их параметров подчиняется
нормальному закону [15]. Используя правило 3s
(трех сигм), определим по исходным данным диапазоны, в которых лежат значения
сопротивлений резисторов:
Когда значения параметров элементов
имеют нормальное распределение, и элементы при создании схемы выбираются
случайным образом, результирующее значение Rеявляется
функциональной переменной, распределенной так же по нормальному закону
[12, 15], причем дисперсия результирующего значения, в нашем случае
Поскольку результирующее значение Rераспределено по нормальному закону, то, воспользовавшись правилом 3s , запишем
где
Таким образом
Данный пример показывает, что при увеличении количества последовательно соединенных элементов результирующая погрешность уменьшается. В частности, если суммарная погрешность всех отдельных элементов равна ± 600 Ом, то суммарная результирующая погрешность равна ± 374 Ом. В более сложных схемах, например в колебательных контурах, состоящих из индуктивностей и емкостей, отклонение индуктивности или емкости от заданных параметров сопряжено с изменением резонансной частоты, и возможный диапазон ее изменения можно предусмотреть методом, аналогичным с расчетом резисторов [15]. 3.5.4. Пример определения показателей надежности неремонтируемого объекта по опытным данным Пример. На испытании находилось Nо = 1000 образцов однотипной невосстанавливаемой аппаратуры, отказы фиксировались через каждые 100 часов. Требуется определить Исходные данные и результаты расчетов
Решение. Согласно формуле (2.1) для любого отрезка времени, отсчитываемого от t = 0,
где ti - время от начала испытаний до момента, когда зафиксировано n(ti) отказов. Подставляя исходные данные из табл. 3.1, получим:
Воспользовавшись формулой (2.9), получим
значение
.................................................................................................................
Средняя наработка до отказа, при условии отказов всех No объектов, определяется по выражению
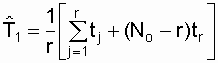 при
r
Ј Nо
, (3.16) при
r
Ј Nо
, (3.16)где tj - наработка до отказа j-го объекта
( j принимает значения
Полагаем, что последний отказ зафиксирован в момент окончания эксперимента (tr = 1500). На основе экспериментальных данных суммарная наработка объектов до отказа равна
где
В результате
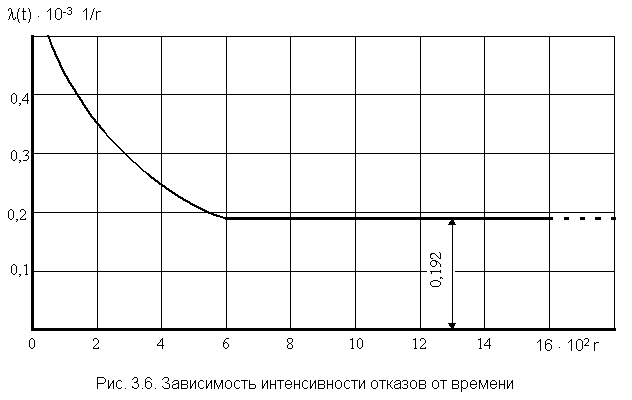
Примечание: обоснование расчетов По полученным данным (см. табл. 3.1) построим график l(t). Из графика видно, что после периода приработки t і 600 ч интенсивность отказов приобретает постоянную величину. Если предположить, что и в дальнейшем l будет постоянной, то период нормальной эксплуатации связан с экспоненциальной моделью наработки до отказа испытанного типа объектов. Тогда средняя наработка до отказа
Таким образом, из двух оценок средней
наработки до отказа
В заключение по данному примеру отметим, что определение средней наработки до отказа по формуле (2.7), когда r << Nо, дает грубую ошибку. В нашем примере
Если вместо Nо поставим
количество отказавших объектов
В последнем случае не отказавшие за
время испытания объекты в количестве Nо - r = 1000-315 = 685
шт. вообще в оценку не попали, то есть была определена средняя наработка
до отказа только 315 объектов. Эти ошибки достаточно распространены в практических
расчетах.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
web-master:
Алхасов М. msh1980@narod.ru |
Руководитель проекта
Ксенофонтов А.С. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

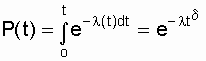 ,
(3.3)
,
(3.3)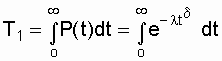 .
(3.4)
.
(3.4)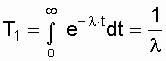 .
(3.6)
.
(3.6)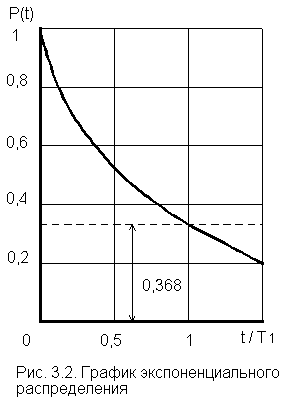
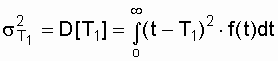 (3.8)
(3.8)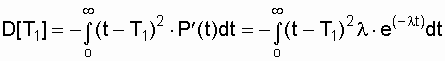 .
(3.9)
.
(3.9)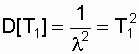 .
(3.10)
.
(3.10)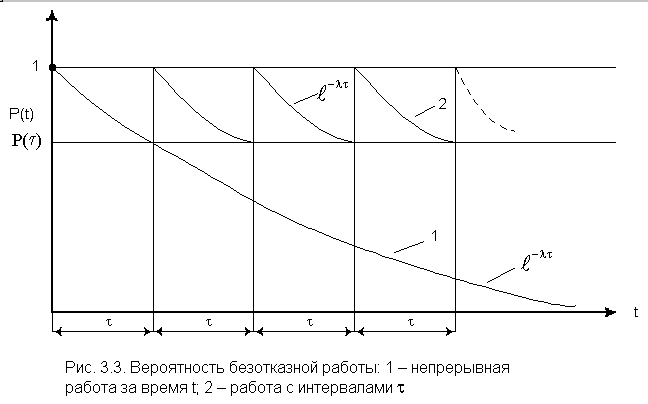
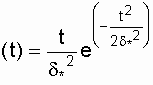 ,
(3.11)
,
(3.11)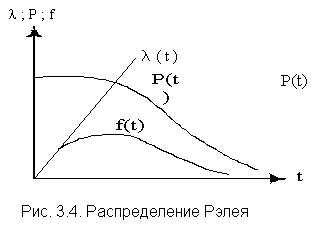
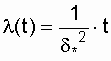 .
.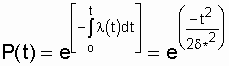 .
(3.12)
.
(3.12)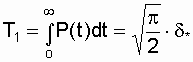 .
(3.13)
.
(3.13)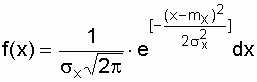 ,
(3.14)
,
(3.14)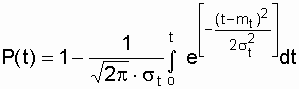 ,
(3.15)
,
(3.15)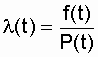 .
.
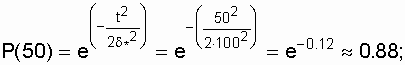
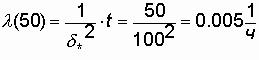 ;
;
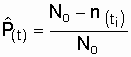 ,
- по формуле Гаусса
,
- по формуле Гаусса
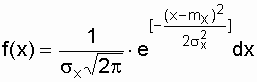
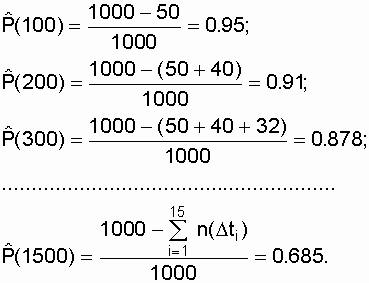
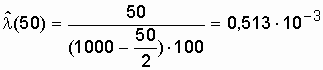 ;
;
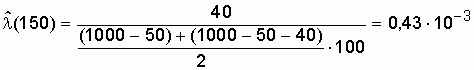 ;
;
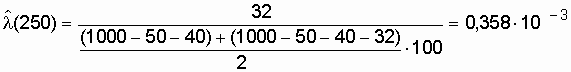 ;
;
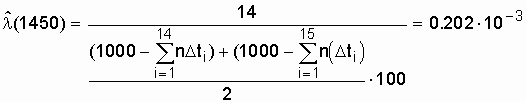 .
.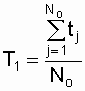 ,
,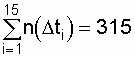 объектов.
Поэтому по полученным опытным данным можно найти только приближенное значение
средней наработки до отказа. В соответствии с поставленной задачей воспользуемся
формулой из [13]:
объектов.
Поэтому по полученным опытным данным можно найти только приближенное значение
средней наработки до отказа. В соответствии с поставленной задачей воспользуемся
формулой из [13]: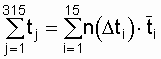 ,
,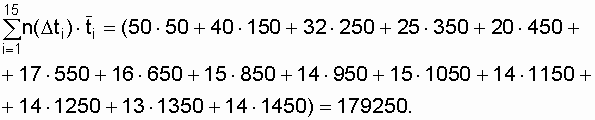
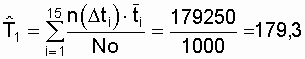 ч.
ч.