|
ФИиУ
Надёжность
КБГУ
КБГУ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7.
Надежность восстанавливаемых систем
7. НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ Сложные технические объекты (системы), рассчитанные на длительный срок службы, создаются, как правило, ремонтируемыми. В разделе 2 дано толкование основных показателей надежности восстанавливаемых объектов (элементов): средняя наработка на отказ; параметр потока отказов; среднее время восстановления; интенсивность восстановления; коэффициенты готовности и оперативной готовности. В данном разделе рассматривается методика анализа надежности восстанавливаемых систем при различных схемах включения элементов. Переход системы из неработоспособного (предельного) состояния в работоспособное осуществляется с помощью операций восстановления или ремонта. К первым, в основном, относятся операции идентификации отказа (определение его места и характера), замены, регулирования, заключительных операций контроля работоспособности системы в целом. Переход системы из предельного состояния в работоспособное осуществляется с помощью ремонта, при котором происходит восстановление ресурса системы в целом. Рассмотрим, к примеру, вакуумный выключатель. Вакуумная камера, не подлежащая восстановлению, при отказе заменяется исправной, то есть восстановление работоспособности выключателя происходит путем замены отказавшей камеры. При отказе в том же выключателе электромагнитного (или пружинного) привода восстановление работоспособности выключателя может производиться путем ремонта привода или замены его исправным. В обоих случаях требуется произвести регулировку привода и проверить функционирование выключателя в целом, осуществив контрольные операции "включить"-"отключить". При анализе используем ряд наиболее часто вводимых допущений.
Данная система с интенсивностью l стремится принять состояние отказа, а с интенсивностью m - перейти в работоспособное состояние. В табл. 7.1 даны заводские параметры l и m для силовой высоковольтной аппаратуры. Таблица 7.1
Обозначим устойчивые состояния системы индексами: 1 - отказ, то есть система находится в состоянии восстановления с интенсивностью восстановления m = const; 0 - работоспособное состояние с параметром
потока отказов
Для анализируемой системы с учетом принятых допущений возможны четыре вида перехода из состояния в момент времени t в состояние в момент времени (t + D t):
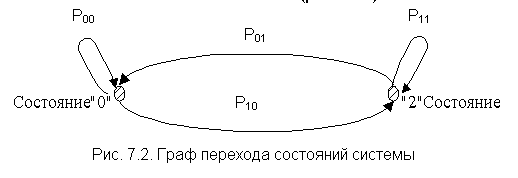
Указанные переходы можно представить
в виде графа перехода состояний системы с восстановлением (рис. 7.2).
Графу перехода состояний [13] соответствует матрица переходных вероятностей 2 х 2:
Диагональные элементы этой матрицы соответственно определятся как вероятность безотказной работы на отрезке Dt:
и вероятность продолжения восстановления системы на отрезке Dt :
Воспользуемся формулой разложения функции
В высоконадежных элементах l<
Таким образом, запишем
Соответственно
Из свойств матрицы следует, что сумма элементов каждой строки матрицы равна единице, как сумма вероятностей появления несовместимых составляющих полную группу событий [13], откуда следует: Р00(D t) + Р01(D t) = 1; Р01 = 1 - Р00(D t) = l D t + 0(D t); Р11(D t) + Р10(D t) = 1; Р10 = 1 - Р11(D t) = m D t + 0(D t). Для составления уравнений вероятностей состояний системы следует записать формулу полной вероятности для каждого столбца матрицы [11, 13, 21]:
где P0(t) - вероятность нахождения системы в нулевом (работоспособном) состоянии в момент времени t; P1(t) - вероятность нахождения системы в состоянии "1" (отказа) в момент времени t. Используем запись производной функции f(x):
и по аналогии с этим выражением для нашего случая запишем:
В эти выражения подставим раскрытые
формулы полных вероятностей
При начальных условиях Р0(t = 0) = 1; Р1(t = 0) = 0, в начальный момент времени (t = 0) восстанавливаемая система работоспособна - находится в состоянии "0". Решение дифференциальных уравнений дает
Вероятность работоспособного состояния системы в момент времени t представляет собой функцию готовности G(t). Функция готовности - это вероятность работоспособного состояния восстанавливаемой системы в определенный момент времени t. Этот показатель является комплексным показателем надежности, оценивающим два свойства системы - безотказность и ремонтопригодность. Заметим, что G(t) дает оценку не за весь период от 0 до t, а только в заданный момент времени t, поскольку до этого система могла находиться как в работоспособном (0), так и в неработоспособном (1) состояниях. На рис. 7.3 построен график:
Предположив l
= const, можно наглядно увидеть насколько повысится надежность системы
за счет увеличения m
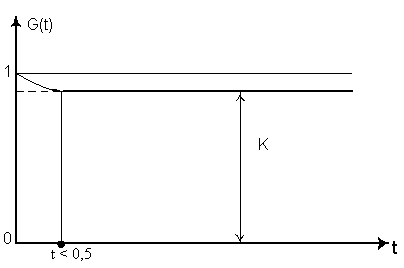
(сокращения времени восстановления Определим предельное значение G(t)по выражению (7.3):
Асимптотическое значение функции готовности при t (r) Ґ и есть коэффициент готовности. Таким образом, коэффициент готовности представляет собой вероятность того, что система окажется работоспособной в произвольный момент времени, кроме планируемых периодов, в течение которых использование системы по назначению не предусматривается.
Пример. Имеется восстанавливаемая
система, у которой параметр потока отказов l
= Решение.
При улучшенной организации труда
По сумме затрат, связанных с улучшением организации труда и экономического эффекта от повышения надежности (улучшения ремонтопригодности), можно сделать вывод о целесообразности такого способа повышения надежности системы. 7.2. Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами Система, состоящая из N последовательных
восстанавливаемых элементов, отказывает, когда отказывает любой из элементов
системы. Предполагаются простейшие потоки отказов и восстановлений
и соответственно при заданных
Пример. Восстанавливаемая система состоит
из трех последовательно включенных элементов с параметрами надежности:
Определить коэффициент надежности. Решение. Подставив заданные значения коэффициентов готовности в выражение КГ системы, получим
Здесь же отметим, что в расчетной практике нередко пользуются формулой вероятности безотказной работы неремонтируемой системы с основным соединением элементов, когда
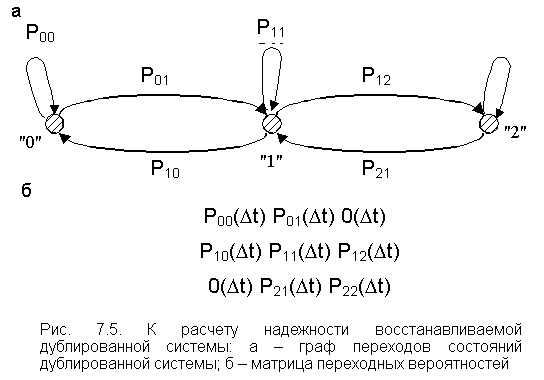
В этом случае 7.3. Надежность восстанавливаемой дублированной системы Рассмотрим систему, для обеспечения надежности которой используется дублирование: основной системе добавляется параллельно такая же система. В обеих системах (цепях) параметры потоков отказов одинаковы, l = const, такая же картина и для потока восстановлений, то есть m = const. Такая дублированная система может находиться в трех состояниях: "0" - обе системы (цепи) работоспособны; "1" - одна цепь восстанавливается, другая работоспособна; "2" - обе цепи восстанавливаются. С точки зрения выполнения функциональных задач, возложенных на систему, состояние "2" соответствует отказу. У этой системы возможны семь видов перехода из состояния в момент времени t в состояние в момент времени t + D t:
Указанные переходы изображены на рис. 7.5 в виде графа переходов состояний.
Графу переходов соответствует матрица
переходных вероятностей
где у - коэффициент, учитывающий состояние
резерва (у = 0 при ненагруженном режиме и у = 1 при нагруженном).
Р00(D t) = 1 - (у + 1) ЧlЧD t. (7.7) С учетом того, что для первой строки матрицы Р00(D t) + Р01(D t) = 1, получим Р01(D t) = 1 - Р00(D t) = (у + 1) Ч lЧD t. (7.8) Элементы второй строки матрицы переходных вероятностей (7.5) соответственно запишутся так: Р10(D t) + Р11(D t) + Р12(D t) = 1;
Элементы третьей строки анализируемой матрицы, с учетом количества ремонтных бригад и многократного восстановления отказавших цепей, соответственно определятся так: Р21(D t) + Р22(D t) = 1;
где r - число ремонтных бригад (r = 1 или r = 2). При дублировании с восстановлением возможны шесть вариантов задач анализа надежности такой системы: 1) система с нагруженным резервом до первого отказа (у = 1, r = 0); 2) система с ненагруженным резервом до первого отказа (у = 0, r = 0); 3) многократно восстанавливаемая система с нагруженным резервом и одной ремонтной бригадой (у = 1, r = 1); 4) многократно восстанавливаемая система с нагруженным резервом и двумя ремонтными бригадами (у = 1, r = 2); 5) многократно восстанавливаемая система с ненагруженным резервом и двумя ремонтными бригадами (у = 1, r = 2); 6) многократно восстанавливаемая система с ненагруженным резервом и одной ремонтной бригадой (у = 0, r = 1). Для определения Р0(t), Р1(t),
где Для этого на основе свойств столбцов матрицы необходимо записать выражения формул полных вероятностей Р0(t + D t), Р1(t + D t), Р2(t + D t), затем записать производные для выражений вероятностей нахождения системы в состояниях "0", "1", "2" и свести их в систему уравнений:
Формулы полных вероятностей запишутся на основе матрицы (7.5) соответственно: по первому столбцу по второму столбцу по третьему столбцу Подставив в эти выражения соответствующие значения переходных вероятностей, получим систему из трех дифференциальных уравнений (7.15) с четырьмя постоянными коэффициентами l , m , r, у. Определение искомых вероятностей пребывания
системы в состояниях "0", "1" и "2" в момент времени t производится при
следующих начальных условиях: Р0(t = 0) = 1; Р1(t
= 0) = 0; Р2(t = 0) = 0, то есть система первоначально включается
в работу с обоими исправными цепями. Решение системы (7.15) подробно изложено
в специальной литературе, например в [13]. Искомое выражение функции готовности
анализируемой системы при найденных значениях Р0(t), Р1(t),
Р2(t) на основе известного свойства
Анализируемая система получается высоконадежной.
Даже в нерезервированной восстанавливаемой системе при Используя данные [13], запишем коэффициенты готовности дублированной системы с многократным восстановлением с одной (r = 1) и двумя (r = 2) ремонтными бригадами:
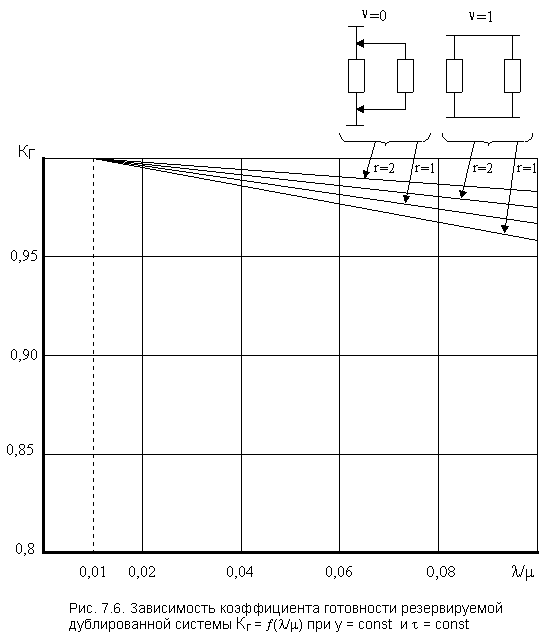
На рис. 7.6 представлены графики коэффициента
готовности Из графика видно, что введение резервирования
в восстанавливаемую систему дает существенное приращение надежности системы
при относительно невысокой надежности основной цепи. К примеру, при
Например, в высоковольтной электроустановке
с показателями безотказности и ремонтопригодности Т = 20000 ч, tв
=100
ч ( Таким образом, при относительно высоком
уровне надежности исходной системы (схемы) выигрыш в надежности при переводе
схемы с режима у = 1 на режим у = 0 ощутимого результата не дает. При эксплуатации,
например двухтрансформаторной подстанции, когда средняя интенсивность отказов
(параметр потока отказов) одной трансформаторной цепи l
< 0,2 1/год, интенсивность восстановления m
> 0,01 1/ч, (
где Выбирать необходимо такую схему включения трансформаторов, которая связана с меньшей потерей мощности. Если подстанция имеет в течение суток нагрузку то высокую, то низкую в четко выраженные интервалы времени, то возникает экономическая целесообразность часто изменять схему включения трансформаторов. Расчеты показывают, что в современных трансформаторах напряжением 35; 10,5; 6,3 кВ и мощностью до 10 тыс. кВА, при нагрузке подстанции, превышающей 0,7 мощности одного трансформатора, экономически выгодно переходить на схему нагруженного дублирования (режим у = 1). Для обеспечения такого режима работы подстанции необходимы циклостойкие выключатели (например вакуумные), способные переключаться под рабочей нагрузкой тысячи раз [14]. Это особенно характерно для подстанций, где преобладает коммунально-бытовая нагрузка, при которой ярко выражены часы максимальной нагрузки (обычно с 7.00 до 9.00 и с 18.00 до 21.00 часа местного времени). В оставшееся время суток нагрузка многократно снижается, и тогда выгодно включать только один трансформатор (режим у = 0). В связи с этим следует отметить, что в установках, где часто меняется нагрузка в широком диапазоне особо эффективны будут тиристорные выключатели рабочих токов, у которых нет технических ограничений по количеству операций (циклов) "включить"-"отключить". Такие высоковольтные восстанавливаемые
дублированные установки, как кабельные линии и воздушные линии электропередачи
должны работать по схеме нагруженного дублирования. При этом, как это было
показано выше, достигается экономический эффект от снижения потери энергии,
и сохраняется высокая надежность электропередачи.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
web-master:
Алхасов М. msh1980@narod.ru |
Руководитель проекта
Ксенофонтов А.С. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
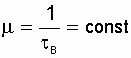 ,
см. 2.3.2.
,
см. 2.3.2.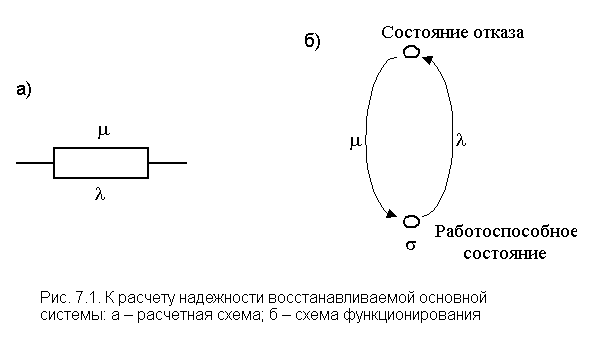

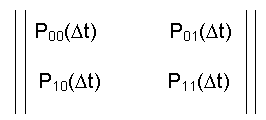 (7.1)
(7.1)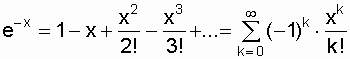 .
.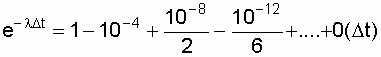 .
.
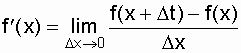
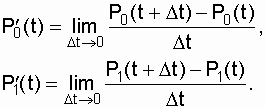
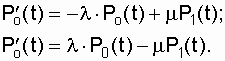
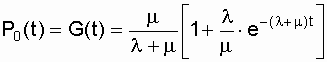 .
(7.3)
.
(7.3)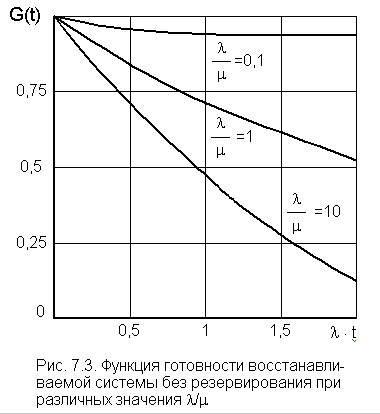
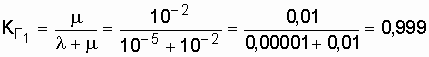 .
.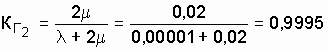 .
.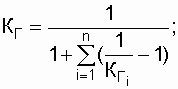
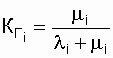
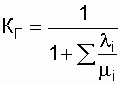 .
.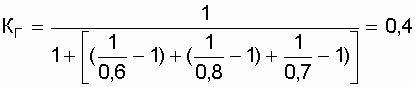 .
.
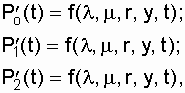 (7.14)
(7.14)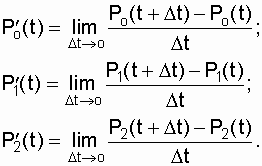 (7.15)
(7.15)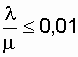
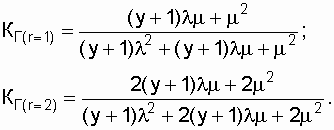
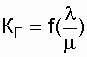 для различных
схем использования резерва и количества ремонтных бригад.
для различных
схем использования резерва и количества ремонтных бригад.
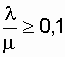 заметен
прирост надежности даже при введении второй ремонтной бригады (r = 2).
Но по мере роста надежности исходных цепей эффект от введения второй бригады
снижается, а при
заметен
прирост надежности даже при введении второй ремонтной бригады (r = 2).
Но по мере роста надежности исходных цепей эффект от введения второй бригады
снижается, а при 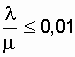 на
графике уже невозможно увидеть различия значений коэффициента готовности
не только при изменении количества ремонтных бригад, но и при переходе
со схемы нагруженного дублирования к дублированию замещением. Так при
на
графике уже невозможно увидеть различия значений коэффициента готовности
не только при изменении количества ремонтных бригад, но и при переходе
со схемы нагруженного дублирования к дублированию замещением. Так при 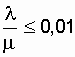 отношение
значения коэффициента готовности схемы дублированной замещением к значению
коэффициента готовности схемы нагруженного дублирования, при одной ремонтной
бригаде в обоих вариантах равно
отношение
значения коэффициента готовности схемы дублированной замещением к значению
коэффициента готовности схемы нагруженного дублирования, при одной ремонтной
бригаде в обоих вариантах равно
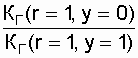 =1,0001.
=1,0001.
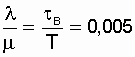 ), использование схемы
нагруженного дублирования повышает надежность установки до
), использование схемы
нагруженного дублирования повышает надежность установки до 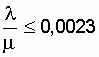 ) схема включения
резервного трансформатора подстанции (нагруженное дублирование или дублирование
замещением) должна определяться по фактическому значению потери мощности
в трансформаторах, а не по уровню надежности. Как известно, потеря мощности
в трансформаторе
) схема включения
резервного трансформатора подстанции (нагруженное дублирование или дублирование
замещением) должна определяться по фактическому значению потери мощности
в трансформаторах, а не по уровню надежности. Как известно, потеря мощности
в трансформаторе